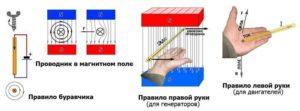
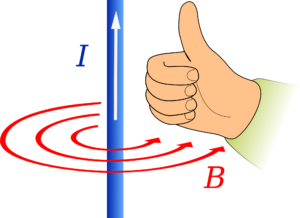
Формулировки правила буравчика (винта) или правила правой руки для специальных случаев
Выше упоминалось о том, что все разнообразные формулировки правила буравчика (винта) или правила правой руки (и другие подобные правила), в том числе все упоминаемые ниже, не являются необходимыми. Их не обязательно знать, если знаешь (хотя бы в каком-то одном из вариантов) общее правило, описанное выше и знаешь порядок сомножителей в формулах, содержащих векторное произведение.
Однако многие из описанных ниже правил хорошо приспособлены к специальным случаям их применения и поэтому могут быть весьма удобны и легки для быстрого определения направления векторов в этих случаях [8] .
Правило правой руки или буравчика (винта) для угловой скорости
Правило буравчика (винта): Если вращать винт (буравчик) в том направлении, в котором вращается тело, он будет завинчиваться (или вывинчиваться) в ту сторону, куда направлена угловая скорость.
Правило правой руки:Если представить, что мы взяли тело в правую руку и вращаем его в направлении, куда указывают четыре пальца, то оттопыренный большой палец покажет в ту сторону, куда направлена угловая скорость при таком вращении.
Правило правой руки или буравчика (винта) для момента импульса
Полностью аналогичны правила для определения направления момента импульса, что неудивительно, поскольку момент импульса пропорционален угловой скорости с положительным коэффициентом [9] .
Правило правой руки или буравчика (винта) для момента сил
Правило буравчика (винта): Если вращать винт (буравчик) в том направлении, в котором силы стремятся повернуть тело, винт будет завинчиваться (или вывинчиваться) в ту сторону, куда направлен момент этих сил.
Правило правой руки: Если представить, что мы взяли тело в правую руку и пытаемся его повернуть в направлении, куда указывают четыре пальца (силы, пытающиеся повернуть тело направлены по направлению этих пальцев), то оттопыренный большой палец покажет в ту сторону, куда направлен вращающий момент (момент этих сил).
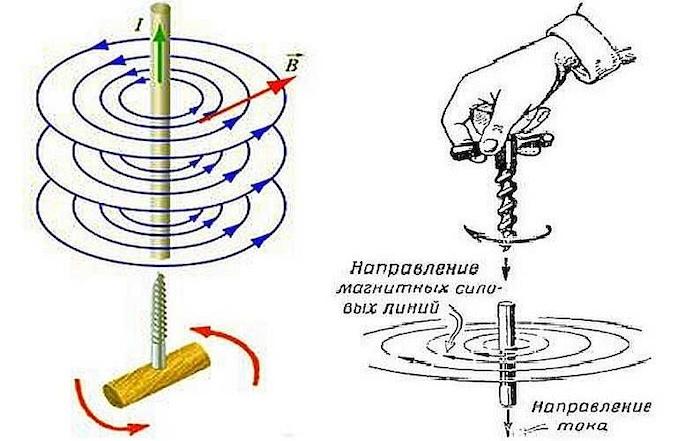
Правило буравчика для прямого и кругового тока
Правило буравчика для прямого и кругового тока
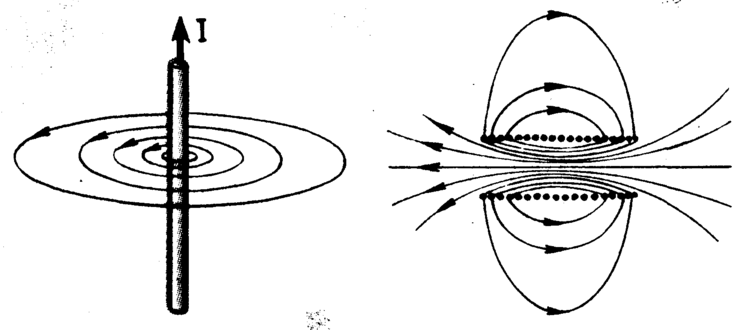
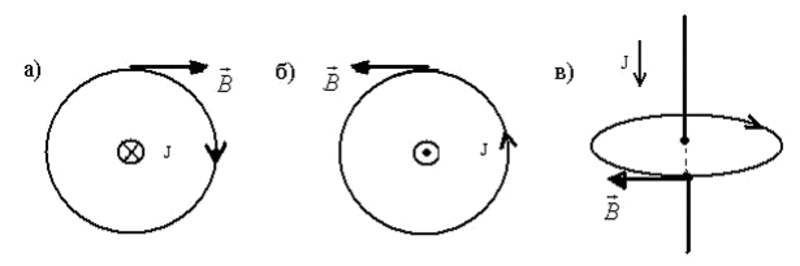
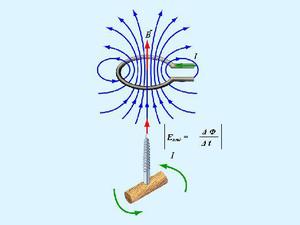
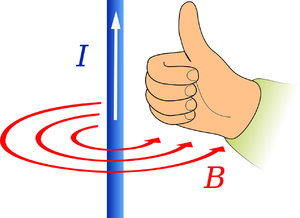
Если создаваемое в пространстве магнитное поле происходит от прямолинейного проводника с током, то магнитная стрелка в любой точке поля будет устанавливаться по касательной к кругам, центры которых находятся на оси проводника, а плоскости — под прямым углом к проводнику.
В этом случае курс вектора МИ определим с помощью правила правого штопора (винта), т. е. при вращении штопора таким образом, чтобы он поступательно двигался по курсу силы тока в проводе, вращение головки штопора (винта) совпадает с направлением вектора магнитной индукции B.
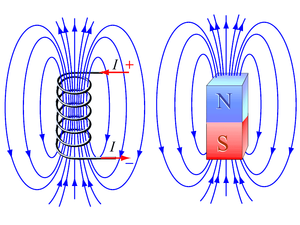
Из второго рисунка усматривается, что магнитные линии (МЛ) в форме кругов замыкаются вокруг проводника с током. В плоскость кругового проводника МЛ входят с одной стороны, а с другой выходят. МП кругового тока похоже на поле короткого магнита, ось которого совпадает с перпендикуляром к центру плоскости контура.
Направление поля КТ можно определить, пользуясь ПБ. Инструмент нужно установить по оси кругового тока под прямым углом к его плоскости. Вращая рукоятку по направлению тока в контуре, можно понять, какое будет направление у МП.
Правило правой руки для угловой скорости
Формулировка ППР для определения угловой скорости (УС) следующая: если кистью правой руки обхватить ось вращения таким образом, чтобы пальцы руки сходились с направлением тангенциальной скорости (ТС), то отогнутый большой палец укажет сторону вектора УС ω.
Как известно, крутящееся колесо имеет не только УС, но и УУ, и оно не совпадает с направлением линейной ТС, а находится под углом 90 градусов к плоскости колеса.
Такая формулировка создаёт некоторое замешательство среди неосведомлённых: оказывается, УС ω действует вдоль оси крутящегося колеса. При вращении колеса очевидно, что единственной застывшей (неподвижной) точкой считается его центр. В этой связи начало вектора УС принято устанавливать в центре вращающейся окружности.
Вектор УС может меняться лишь по величине. А вот вектор УУ изменяется как по величине, так и по направленности — при ускорении направления векторов УС и УУ совпадают, а при замедлении направленность противоположная.
Для чего применяют правило буравчика
Известно, что электроток — это направленное движение элементарных частиц, переносящих заряд электричества по имеющим электропроводимость проводникам.
Если взять источник электродвижущей силы (ЭДС) с током, идущим по проводу замкнутой цепи, то есть от «плюса» к «минусу», то в окружении проводника происходят вращающиеся по определённому кругу, магнитные кругообороты, конфигурация которых имеет важное значение. Эти крутящиеся поля взаимодействуют друг с другом и могут притягивать или отталкивать проводники к себе и от себя. А зависит это от того, как и в какую сторону вращаются магнитные поля.
Характер такой взаимосвязи был сформулирован Ампером в виде закона, который стал основой для возникновения электромоторов. Без знания ПБ (правила буравчика) невозможно было бы изобрести электромотор. В этом заключается экспериментальное применение правила.
При расчёте катушек индукции характерным является использование ПБ, а именно с учётом стороны, в которую направлено завихрение, можно будет воздействовать на движущийся ток, в том числе создавать при необходимости противоток.
Правило левой руки
Нельзя объединять и путать с правилом буравчика. Их применяют с разными целями.
Объяснение названия
Явление электромагнитной индукции
После изучения общих принципов и формулировок пользоваться рассмотренными правилами несложно. Ниже подробно представлены методики, которые применяют при работе с электротехническими схемами. В частности, с их помощью определяют направление тока. При необходимости уточняют параметры образованного поля.
Аналогичные технологии можно использовать в механике для оценки угловой скорости и других рабочих параметров системы. Изменяются только отдельные компоненты формул. Алгоритмы применения технологий остаются неизменными.
Что определяет
Определяет направление двух сил:
- силы Лоренца;
- силы Ампера.
Сила Ампера: варианты расчета
Прежде чем сформулировать данную величину, необходимо разобраться, что такое понятие сила в физике. Ей называется величина в физике, которая является мерой воздействия всех окружающих тел на рассматриваемый объект. Обычно любую силу обозначают английской буквой F, от латинского fortis, что означает сильный.
Рассчитывается элементарная сила Ампера по формуле:
где, dl – часть длины проводника, B –индукция магнитного контура, I – сила тока.
Рассчитывается также сила Ампера по формуле:
где, J – направление плотности тока, dv– элемент объема проводника.
Формулировка расчета модуля силы Ампера, согласно литературе, звучит так: данный показатель напрямую зависит от силы тока, протяженности проводника, синуса, образуемого между этим вектором и самим проводником угла, и величины значения вектора магнитного контура в модуле. Она и носит название модуля силы Ампера. Формула данного закона математически строится так:
где, B – модуль индукции магнитного контура, I – сила тока, l – длина проводника, α – образуемый угол. Максимальное значение будет при перпендикулярном их пересечении.
Показатель измеряется в ньютонах (условное обозначение – Н) или
. Он является векторной величиной и зависит от вектора индукции и тока.
Существуют и другие формулы для расчета силы Ампера. Но на практике они достаточно редко востребованы и тяжелы для понимания.
Сила тока
Иногда чтобы рассчитать закон Ампера, для начала нужно вычислить силу тока. Существуют несколько формул расчета данной величины. Для расчета ее величины используют:
- закон Ома для полного участка цепи и ее части,
- отношение напряжения и суммы сопротивлений,
- отношение мощности и напряжения.
Самым популярным является отношение количество заряда прошедшего за единицу времени через определенную поверхность к размеру этого интервала. Графически формула выглядит следующим образом:
Чтобы найти этот показатель можно пользоваться законом Ома для участка цепи. Он гласит следующее: величина этого показателя равна отношению приложенного напряжения к сопротивлению на измеряемым участке цепи. Записывается формула этого закона следующим образом:
Определить ее также можно, применив формулу закон Ома для полной цепи. Звучит он так: эта величина является отношением приложенного напряжения в цепи и суммы внутреннего сопротивления источника питания и всего сопротивления в цепи. Формула выглядит так:
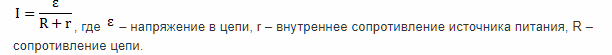
Рассчитать данную величину можно, в случае если известны мощность и напряжение.
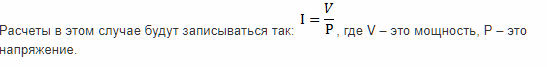
Важно! Применение каждой конкретной формулы зависит от имеющихся в распоряжении данных.
Согласно утвержденной МСЕ, измеряется сила тока в амперах, и обозначается А (в честь ученого, открывшего ее). Но это не единственный способ обозначения данной величины. Дополнительно измеряется сила тока в Кл/с.
Изучая в общеобразовательных учреждениях данный материал, ученики быстро забывают, как применять правила левой и правой руки, и для чего они вообще нужны. Также часто они не помнят в чём измеряют указанные величины. Ознакомившись с рассмотренным выше материалом, не должно возникнуть трудностей с применением рассмотренных правил и законов на практике.
Правило буравчика
Правило правой руки
Общие правила
Существует несколько для вариантов, чтобы указать направление перпендикулярного отрезка к двум исходным векторам и определить ориентацию базиса. В физике есть такие важные направления:
- оборотов тела вокруг центра движения;
- силового вектора магнитного поля в выбранной точке.
Выбор пути аксиальной величины является условным, но он происходит одинаково, поэтому в конечном значении знак остается постоянным. Правила и способы помогают сохранять единый выбор:
Правило буравчика. Провод помещается в руку, при этом четыре пальца сжимаются в кулак. Главный палец, который располагается вертикально, покажет путь передвижения заряженных электронов (тока). Остальные пальцы, которые ставятся параллельно друг другу, определят направление передвижения электромагнитных линий.- Правило правой руки. При помещении исследуемого кабеля в руку сжатые пальцы показывают путь линий силового поля, а большой — направление тока. При поступательном перемещении проводника вдоль линий, которые определяют напряженность, их движение направлено в ладонь. Вытянутый перпендикулярно большой палец совпадает с перемещением стержня. Если раскрыть кулак, то прямые пальцы определят курс индукционного тока.
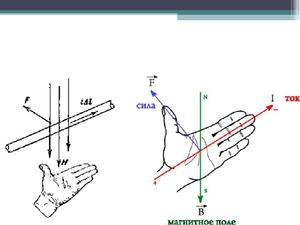
- Правило левой руки. Рука располагается так, чтобы четыре пальца показывали направление движения электронов. Путь индукционных линий направлен в ладонь. Отогнутый палец показывает действие силы на провод. Закон действует для отклонения проводникового стержня, справа и слева от которого располагаются магниты, а он находится под током.
С помощью этих правил выбирается направление векторного произведения и базисов (или одного из двух взаимосвязанных понятий). Прием используется для определения направлений основных величин взамен применения остальных методов, если иметь представление о порядке расположения множителей в соответствующих формулах.
Способы выбора правила сочетаются между собой для вычисления положительного пути произведения векторов и базиса (координатной системы) в пространстве. Базис определяется как скоординированный векторный набор, при этом любой вектор в пространстве представляется в едином варианте линейного соотношения векторов из этого пакета.
Использование правила буравчика из физики приводит к главным выводам:
движущийся стержень, стационарный магнит, заряженные электроны располагаются в электромагнитном силовом поле;- на положительные и отрицательные частицы оказывается воздействие электромагнитного фона;
- перемещающийся проводник становится ориентиром для передвижения заряженных электронов, значит силовое поле действует на электрический шунт.
Можно применять специальные правила для определения направляющих характеристик стержня, который движется в электромагнитном поле. Этими формулировками пользуются в различных конкретных ситуациях, но они являются менее общими по значению.
Правая и левая системы координат
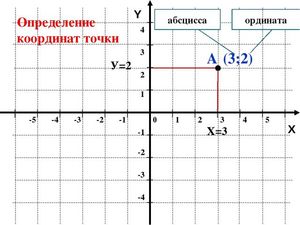
Чтобы выяснить направление прямоугольных векторных координат, которые используются для показания отрезков любого курса, исходят из правила для чайников, что абсцисса и ордината направленного луча находятся в исходной точке пространства и совпадают с характеристиками их окончания.
Для случаев, когда координаты не совпадают, нужно сделать:
перенос луча так, чтобы его начальная точка находилась в начале координатного пространства, таким образом, абсцисса и ордината истока отрезка совпадают с координатами его окончания;- вычитание из координатных показателей конца луча значение абсциссы и ординаты конца отрезка вместо перемещения начальной точки.
На плоскости прямоугольных координат расположение отрезка совпадает с ортогональной проекцией луча на координатную направляющую ось. Правило буравчика позволяет применять правый базис, но отход от негласного закона оговаривается отдельно. Эти правила условны, но сочетание векторов устанавливается так, что для базиса декартовой прямоугольной плоскости с одинаковым масштабированием по любым осям выполняются следующие законы:
- левые базисы вступают во взаимодействие, если применение правосторонних скоплений неудобно или не представляется возможным;
- зеркальное отображение правого сочетания базиса является копией левого набора векторов.
Правила согласовываются между собой для определения курса векторного произведения и законов построения (выбора) положительного набора векторных отрезков.
Для векторного произведения
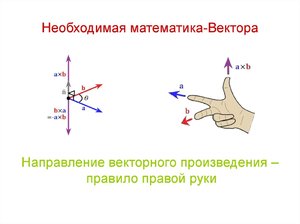
Правило буравчика и правой руки для векторного результата гласит, что, если изобразить отрезки так, чтобы совпадали их истоки, и поворачивать первый вектор по наиболее краткому пути по отношению ко второму лучу, то винт будет вращаться в направлении произведения векторов.
В качестве винта подразумевается буравчик с правой нарезанной резьбой или с правым винтиком на конце, который встречается часто в списке рабочих инструментов. Этот закон можно переформулировать для стрелки часов, так как правое вращение винта идентично перемещению указателя на циферблате.
Вам это будет интересно Расчёт и таблицы подбора сечения кабеля по мощности и току
Для векторного произведения через стрелку на циферблате правило применяется, если изобразить отрезки так, чтобы их истоки совпадали. При этом второй луч вращается кратко по траектории ко второму вектору из набора. Направление векторного произведения будет идти к наблюдателю, если он стоит так, что обороты видит по часовому указателю. Буравчик закручивается вглубь часов.
Если при таком положении наблюдателя и однотипном вращении с предыдущим случаем ставятся пальцы кисти справа, как бы сжимая поворачивающийся стержень, то они указывают направление витков. Палец, который располагается под углом 90°, определяет курс векторного произведения.
Если векторы изображаются так, что их истоки находятся в одной точке, палец правой кисти ставится по первому вектору-множителю, а указательный — параллельно второму вектору, то средний приблизительно укажет курс векторного произведения для закона буравчика. Физика в таком случае определяет направление:
- луча электромагнитных линий;
- движения электронов, заряженных отрицательно и положительно;
- силы индукции.
Соотношение отрезков, абсцисс и ординат
Векторное соотношение двух отрезков, которые взаимодействуют в трехмерном пространстве, определяется лучом, расположенным перпендикулярно обоим начальным потокам. Длина произведения векторов равняется значению площади параллелограмма между начальными отрезками. Направление этих двух лучей выбирается так, чтобы три по порядку расположенных вектора из набора и результативных отрезков были правыми. Результат умножения векторов коллинеарного типа приравнивается к нулю, если один из них является отрезком с нулевым значением.
Для нахождения произведения пространственных векторов следует определить ориентацию участка, а именно разобраться в том, какие три отрезка относятся к правому и левому положению. При этом необязательна привязка к координатной системе. При выбранной ориентации пространственного участка результат произведения множительных векторов не зависит от левосторонней или правосторонней системы числовых направляющих.
Формулы отличаются по знаку для нахождения координат произведения лучевых векторов через ординаты и абсциссы начальных отрезков в левой и правой системе прямоугольной структуры. Результат сочетания векторов является антикоммутационным, так как в отличие от скалярного результата в итоге имеет также вектор.
Модуль произведения векторов также является результатом перемножения модулей отрезков, если величины располагаются перпендикулярно друг к другу. Значение модуля стремится к нулю в случае коллинеарности лучей. Произведение векторов определяется в физических и технических дополнениях. Например, импульсный момент и действие Лоренца заносятся в данные по форме результата перемножения элементов из векторного набора.
Для упорядоченного набора лучей
Все разнообразные применяемые правила винта или законы обеих рук в электротехнике и физике не являются обязательными к использованию, если направление характеристик электромагнитного поля можно определить основными правилами одновременно со знанием формул для подсчета векторного соотношения.
Малораспространенные правила характерны для особых случаев, когда их использование является удобным для быстрого выявления элементарных показателей системы.
Правила для базиса переписаны в виде:
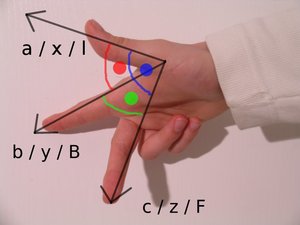
Закон для базиса. Если в базисе присутствуют векторы, которые располагаются параллельно осям x, z, y, то большой палец направляется вдоль первого вектора по оси x. Указательный ставится параллельно второму отрезку по оси y, средний располагается вдоль третьего луча по оси z. После расстановки выявляется, что сочетание векторов относится к правостороннему расположению.- Закон винта (буравчика) для базиса. Если поворачивать винт и векторы так, чтобы первый отрезок стремился ко второму по наименьшему пути, то буравчик направлением кручения покажет курс третьего вектора базиса (когда он правый).
Вам это будет интересно Математическая запись закона Джоуля-Ленца и его применение
Такие манипуляции расширяют возможности определения курса в координатном пространстве. Закон буравчика для базиса может заменить общее правило винта, правой кисти и других. Для его применения у наблюдателя должно быть развито некоторое пространственное воображение, так как требуется мысленно осуществлять поворот нарисованных векторов до того момента, пока они не совпадут с базисом. Набор векторов может при этом располагаться случайно.
Принцип для механического вращения
Отрезок вращения взаимно связывается с вектором угловой скорости поворота и лучом, начинающимся в неподвижной точке, приведенным в искомое положение. Величина определяется как произведение векторов. Угловая скорость представляет собой быстроту оборотов материального элемента вокруг центра.
Угловая скорость выражается:
для поворотов в двухмерном участке пространства — числом;- для трехмерного промежутка — псевдовектором, компоненты которого трансформируются при оборачивании координатной системы и меняют знак противоположно правилам поведения вектора при инверсии;
- в вариантах общего положения — кососимметрической величиной, меняющей знак при перемене индексации.
Для определения курса модуля отрезка применяются правило винта и правой кисти, эффективно используемые в случае нахождения векторного произведения. Иногда этого хватает, но при реальном вращении законы формулируются в запоминающемся и простом варианте для нахождения направлений:
Закон буравчика. Если поворачивать винт в направлении вращения точки, то он завинчивается в сторону курса угловой скорости.- Закон правой руки. Для этого тело берется правой рукой и поворачивается в направлении четырех пальцев, большой палец, который располагается под углом 90°, покажет путь угловой скорости при таком движении вокруг центра.
Для определения направления момента импульса, который меняется прямо пропорционально угловому вращению (скорости) с коэффициентом положительного импульса, применяются правила для нахождения показателей механического кручения.
Определение силового момента
Крутящий и вращательный момент представляет собой физический формат, равный произведению векторов силы и радиуса, проведенных от центральной оси к точке действия силы. Характеристики показывают силовое действие на твердом предмете.
Правила аналогичны предыдущим случаям, но отличаются незначительными деталями:
Правило винта. Если поворачивать буравчик по курсу, куда сила вращает тело, то инструмент будет завинчиваться или вывинчиваться по путям направления силового момента.- Правило правой кисти. Мысленно представляют, что тело в руке, тогда попытка его поворота в направлении вытянутых четырех пальцев (аналогично направляются поворотные усилия) при большом пальце на 90° покажет направление приложения вращательного момента.
Правило правой и левой руки: применение на практике
Рассматривая применение этого закона, начнём с правила правой руки. Если известно направление вектора магнитного поля, при помощи буравчика можно обойтись без знания закона электромагнитной индукции. Представим, что винт передвигается вдоль магнитного поля. Тогда направление течения тока будет «по резьбе», то есть вправо.
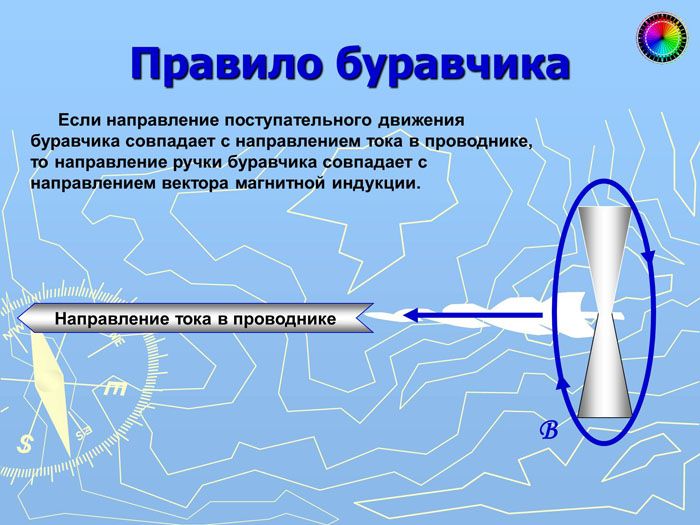
Ещё одно чёткое и понятное объяснение
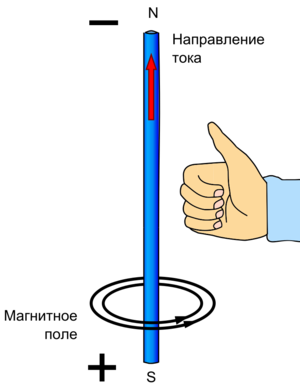
Применение правила правой руки для соленоида
Обратим внимание на постоянный управляемый магнит, аналогом которого является соленоид. По своей сути он является катушкой с двумя контактами. Известно, что ток движется от «+» к «-». Опираясь на эту информацию, берём в правую руку соленоид в таком положении, чтобы 4 пальца указывали направление течения тока. Тогда вытянутый большой палец укажет вектор магнитного поля.
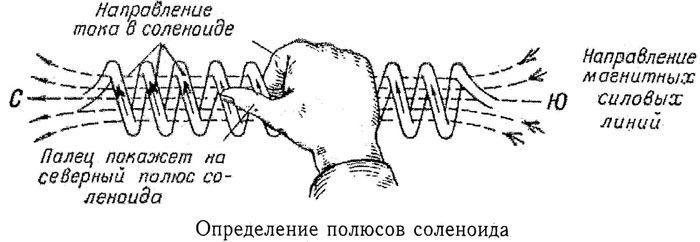
Применение правила правой руки для соленоида
Выводы
Освоить эти способы определения направления сил и полей очень просто. Такие мнемонические правила в электричестве значительно облегчают задачи школьникам и студентам. С буравчиком разберется даже полный чайник, если он хотя бы раз открывал вино штопором. Главное не забыть, куда течет ток. Повторюсь, что использование буравчика и правой руки чаще всего с успехом применяются в электротехнике.
Напоследок рекомендуем просмотреть видео, благодаря которому вы на примере сможете понять, что такое правило буравчика и как его применять на практике.
Видеообзор
https://www.youtube.com/watch?v=zbEzpFAwUI8
